Graph Convolutional Network (GCN)
오늘은 ICLR 2017 에서 나온 논문인 semi-supervised classification with graph convolutional networks 를 읽고
GCN 에 대해서 리뷰하려고 합니다. 그래프를 공부하면서 읽는 첫 논문이라 개인적으로 어려웠습니다.
Abstract 를 읽어보면 논문에서 소개하는 convolutional 모델은 spectral graph convolution의 localized first-order approximation이라고 합니다.
그래프를 통해서 label information이 smoothed 가 된다고 하고 이는 정규화된 Laplacian 행렬을 이용하기 때문에 가능하다고 하는데 전혀 이해가 안갔습니다.
라벨이 있는 노드에 대한 loss와 라벨이 없는 노드에 대한 loss를 같이 구하여 classification task 에 사용하기 때문에 semi-supervised learning 이라고 하는 것 같습니다. 같은 label을 가진 node라면 feature이 유사할 것이다 같은 전제를 두고 label data를 통해 일반적인 특징을 학습하면, unsupervised learning도 가능하다는게 semi-supervised 입니다.
Fast approximate convolutions on graphs
GCN은 다음 layer-wise propagation rule에 따라 계산할 수 있습니다
$$H(l+1)=σ(D̃^{-\frac{1}{2}}Ã D̃^{-\frac{1}{2}} H(l)W(l))$$
- $D̃^{-\frac{1}{2}}Ã D̃^{-\frac{1}{2}}$
뒤에서 설명하겠지만 인접행렬(A) 에 대해 normalize 하여 구한 Laplacian Matrix $L$ 에 대해 eigen-decomposition 을 한 것이고 이를 통해 그래프에 대해 localized spectral filtering 이 가능합니다. - Ã , D̃
인접행렬 A와 degree matrix에 $I_{N}$ 을 더해준 것입니다. 자기 자신 노드에 대한 self-roop 를 추가해준 것으로 이해하면 되는데, node update시 자신에 대한 정보가 제외되지 않는 것을 방지하기 위해서라고 합니다. - $H^0$은 input feature, $H^{1}$은 l레이어에서의 hidden state입니다.
- $W(l)$
layer-specific trainable weight matrix
traditional FC layer 과 유사하고 다음과 같이 2 step 으로 나눠서 볼 수 있습니다.
1. aggregate neighbors
2. pass to a standard neural net

Spectral Graph Convolution
제가 생각하기에 GCN 을 이해하는데 가장 중요한 부분이며 논문의 2.1 의 Spectral Graph convoultion 파트에서는 계속해서 어떻게 $ Z = D̃^{-\frac{1}{2}}Ã D̃^{-\frac{1}{2}}X\theta$ 로 근사할 수 있는지에 대해 설명합니다.
그래프의 노드는 이미지와 달리 'local invariance' 없기 때문에 고정된 사이즈의 filter 를 통해 convolution을 하는 spatial convolution 를 썼을 때 문제가 있다고 합니다. 그래프에서는 고정된 이웃 노드에서만 정보를 받게 되겠죠.
그래프는 Message passing을 통해 시간에 따라 이웃노드의 정보를 aggregate 하여 노드정보가 업데이트됩니다. 아래 그림에서 t시점에 따라 노드가 바뀌는 것을 확인할 수 있습니다.

따라서 Time 기준으로 signal 을 분석하는 게 아니라 frequency 기준으로 노드에 대한 signal 을 분석하자는게 'spectral graph convolution' 의 idea이고 이를 위해서 푸리에 변환(Fourier Transform)을 하게 됩니다.

spectral convolution을 통해서 graph의 특징을 파악하기 위해서는 signal에 대한 푸리에 변환을 하는데, 이를 Laplacian matrix의 eigen-decomposition 을 통해서 쉽게 할 수 있습니다. 왜?
Laplacian matrix 는 L = D - A 인 걸로만 알고 있었는데 이는 쉽게 구하는 방법이고, 그래프에서의 라플라시안 행렬은 'smoothness' 를 의미한다고 합니다.
인접행렬에 대한 정보와 edge 정도를 통해 이웃 노드와의 variation 에 대한 정보를 담고 있고, 이를 signal 로 봤을 때 노드 간 message pass 에서 유사한 노드간의 신호와 상이한 노드간의 신호의 결합 형태로 이해할 수 있습니다.
그리고 eigen-decomposition 을 통해 얻은 '작은' eigenvalue 을 projection 함으로써 가까운 노드에서 오는 signal 을 잘 추출할 수 있습니다.
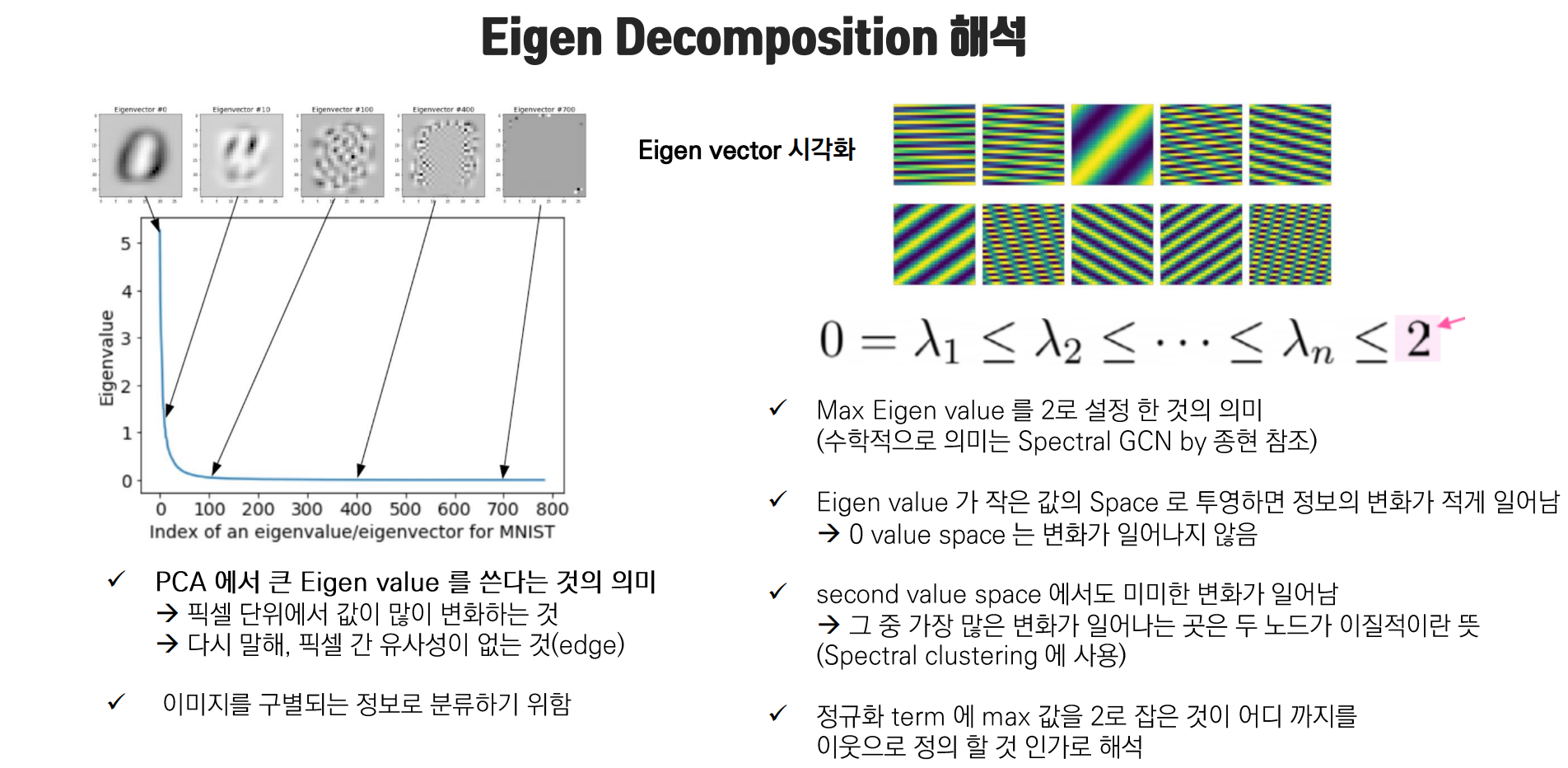
뿐만 아니라 Laplacian matrix 는 symmetric matrix 이고 , symmetric matrix 는 항상 diagonolozation 이 가능하므로 eigenvector 가 orthonormal 합니다.
그런데 푸리에 변환에서는 혼합 signal을 sine 과 cosine 의 직교하는 주파수 성분으로 쪼개어 선형결합을 하는데, laplacian matrix 을 이용하면 쉽게 graph signal을 orthogonal vector 로 분해할 수 있다는 점에서 중요한 성질을 지닙니다.
Transductive GCN 의 한계
- Full batch 학습
H = AX, 한번에 노드 간 이웃을 통합하면서 계산하는데
노드 수가 많아지게 되면 complexity가 비약적으로 상승합니다. - Mini-batch
미니 배치 complexity도 크게 달라지지 않는게, 2-hop layer 만 따져도 노드 수가 전체 노드와
큰 차이가 없어지고 반복 연산을 해야해서 비효율적입니다
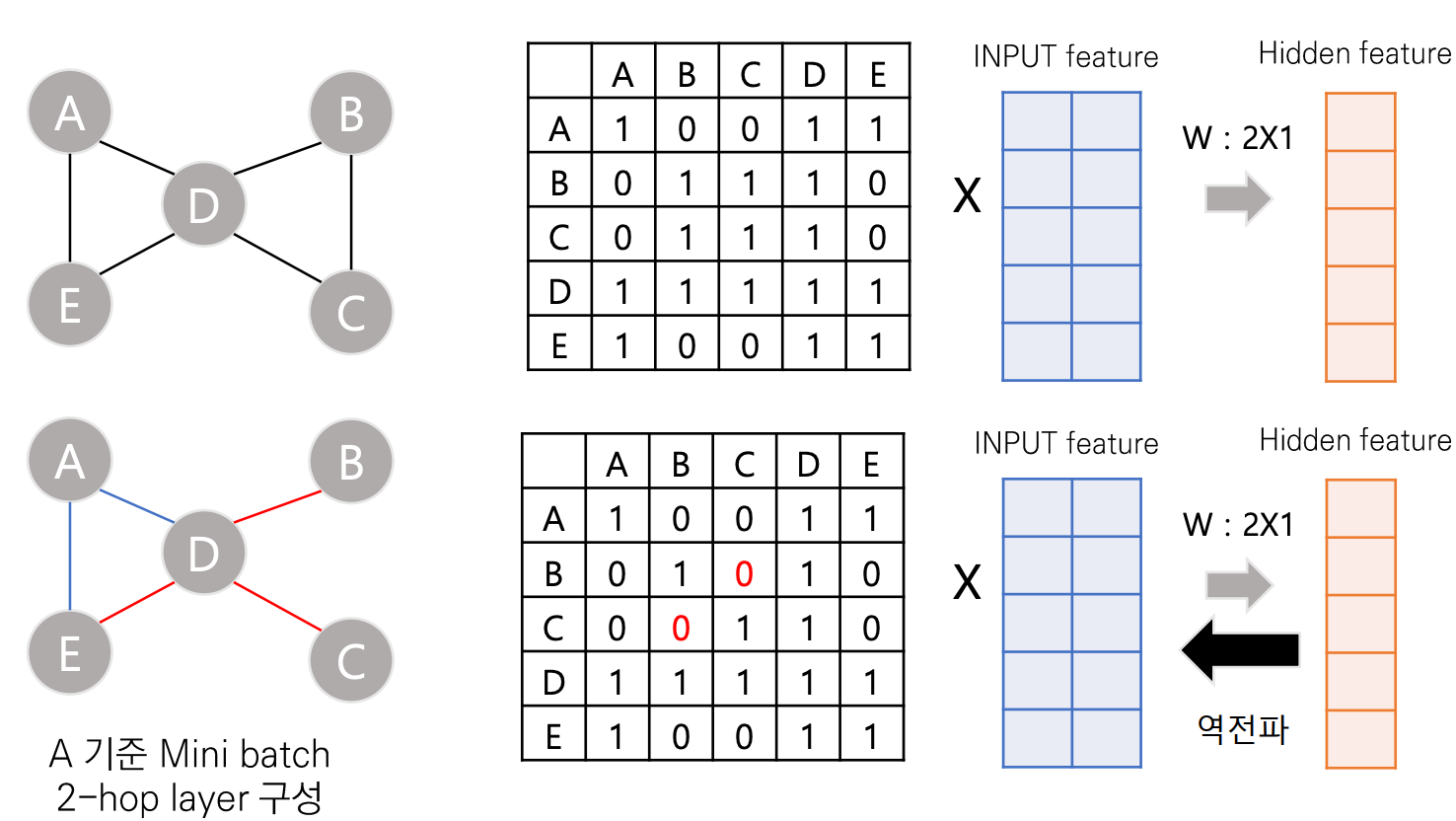
- Transductive → inductive learning
연결된 전체 노드를 사용하지 말고, 샘플링하여 sub graph를 구성하자는 아이디어로
전체 structure 를 계산해야 하기 때문에 normalized degree를 계산하지 않고 sampling 을 통해 aggregate하는
방법이 inductive learning을 사용하는 GraphSAGE 라고 합니다.
- Reference
[Blog]
https://ralasun.github.io/deep%20learning/2021/02/15/gcn/ - [Youtube]
https://www.youtube.com/watch?v=8qTnNXdkF1Q
https://www.youtube.com/watch?v=jBF3Q1lgC3c&t=1031s - https://blog.zakjost.com/post/gcn_citeseer/
'Graph' 카테고리의 다른 글
| 06. Structural properties of Network (0) | 2022.06.04 |
|---|---|
| 05. Node centrality rating on Networks (0) | 2022.06.01 |
| [CS224W] 7. Graph Neural Networks 2: Design Space (0) | 2022.02.26 |
| [CS224W] 5. Label Propagation for Node Classification (0) | 2022.02.08 |
| [CS224W] 3. Node embedding (0) | 2022.02.02 |
댓글
이 글 공유하기
다른 글
-
05. Node centrality rating on Networks
05. Node centrality rating on Networks
2022.06.01 -
[CS224W] 7. Graph Neural Networks 2: Design Space
[CS224W] 7. Graph Neural Networks 2: Design Space
2022.02.26 -
[CS224W] 5. Label Propagation for Node Classification
[CS224W] 5. Label Propagation for Node Classification
2022.02.08 -
[CS224W] 3. Node embedding
[CS224W] 3. Node embedding
2022.02.02