[CS224W] 3. Node embedding
1. Node embedding
기존의 머신러닝 모델에서 그래프를 이용하는 방법은 다음과 같다. input으로 그래프가 주어졌을 때, feature engineering을 통해 structured features를 만들어 ml 알고리즘으로 이를 학습한다.
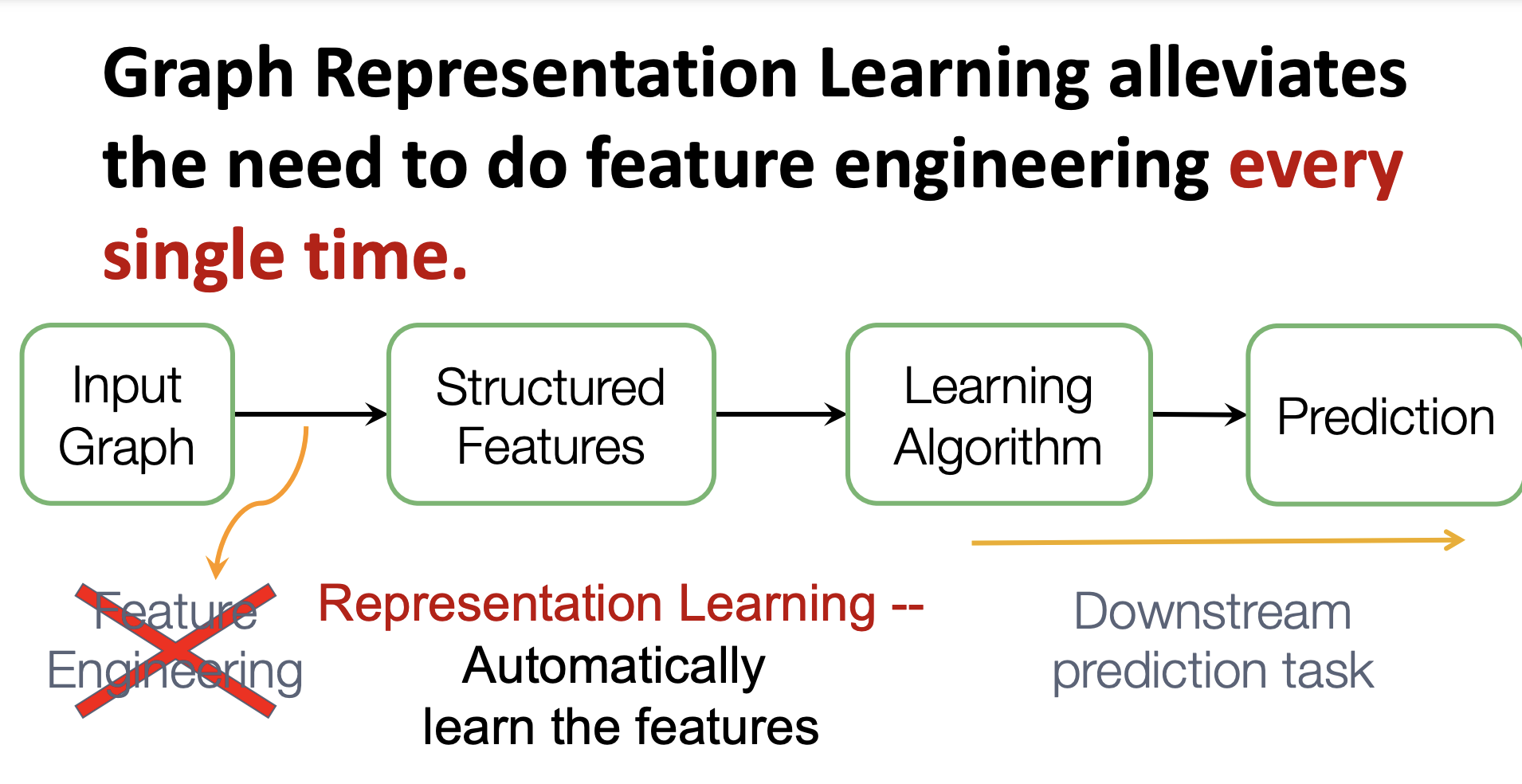
하지만 Graph Representation learning 은 피쳐 엔지니어링을 자동화하기때문에 특정 task 마다 반복되는 작업을 할 필요가 없다. graph 를 잘 표현하는 것은 결국 그래프의 feature를 representation 하는 것이다. 노드 임베딩이란 그래프의 node u를 d차원의 실수 벡터로 표현하는 것이다.
노드를 벡터로 표현할 수 있게 되면, 노드 간의 similarity를 구할 수 있으며 네트워크(graph) 간의 유사성도 구할 수 있다. 뿐만 아니라 앞서 말했던 것 처럼 link prediction, node classification, clustering 등의 task에 independent 하다.
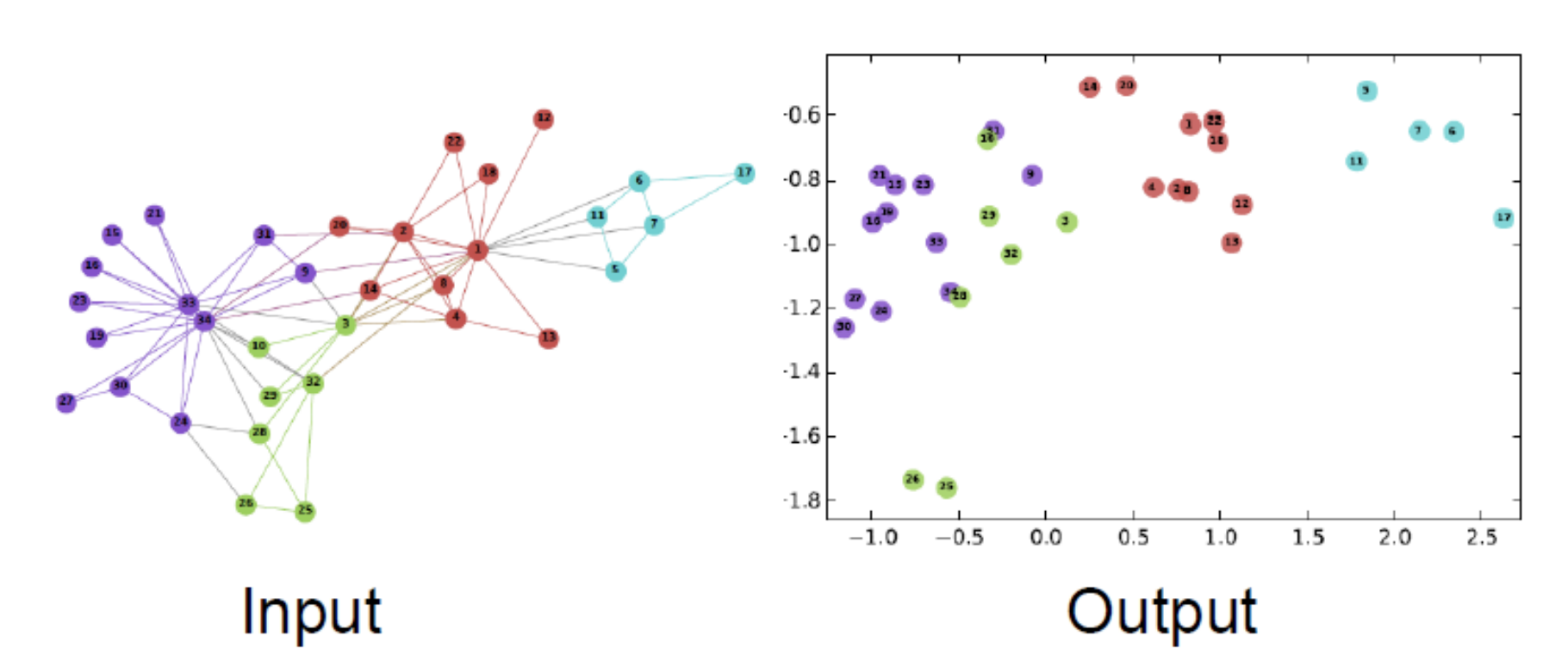
- 노드 임베딩은 unsupervised/self-supervised 기법이다.
- node labels, node features 를 이용하지 않는다
- 네트워크 구조가 보존되도록 임베딩하면서 node의 coordinate set을 예측하는게 목표이다
- 노드 임베딩은 task independent하다
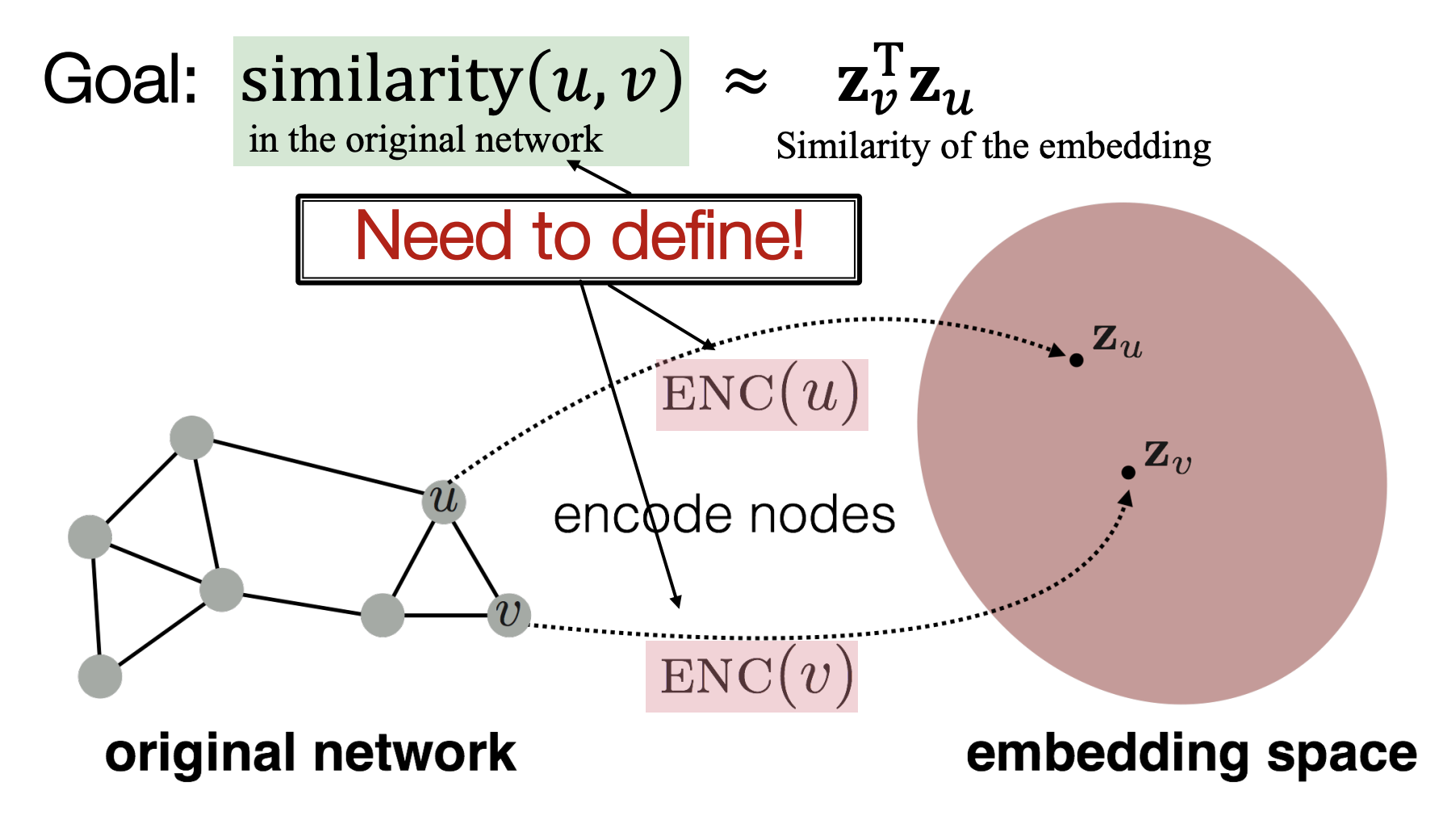
그렇다면 어떻게 임베딩을 할까?
노드 임베딩의 목적은 original network(graph) 에서의 노드간의 유사성이 embedding space에서의 벡터 거리와 잘 대응되도록 하는 것이다. 예시로 두 벡터의 dot-product를 통해 구한 벡터들의 cosine angle은 흔히 유사성의 지표로 이용된다.
<순서>
1. Encoder : maps nodes to embedding
2. 노드 유사성 함수 정의 (graph node간의 유사성)
3. Decoder : maps embeddings to similarity score
4. Optimize : 각 유사도 지표를 최적화
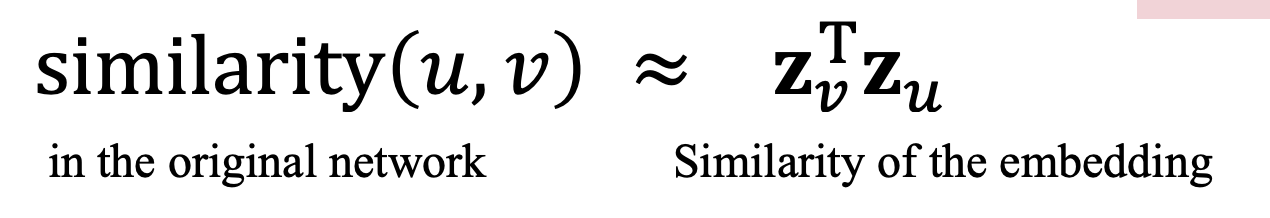
Encoder
여기서 인코더는 단순히 embedding-lookup 이기 때문에 "shallow" Encoding 이라고 표현한다.
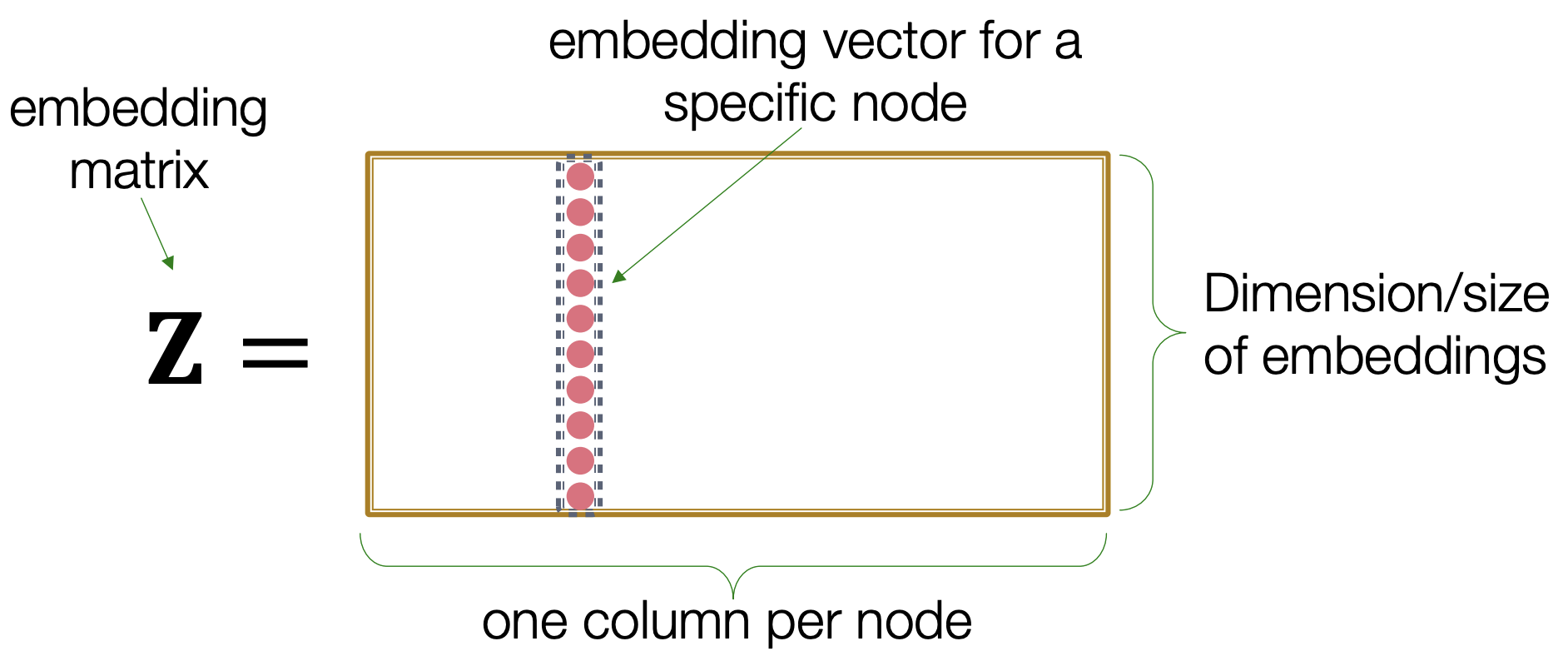
embedding matrix z의 row는 임베딩 차원의 크기이며
column은 각 node에 대한 embedding vector이다.
그래프와 노드의 크기에 따라 matrix가 커지긴 하지만 한번 계산이 되면 쉽게 노드간 연산을 할 수 있다.
2. Random Walk Approaches for Node Embeddings
Deepwalk
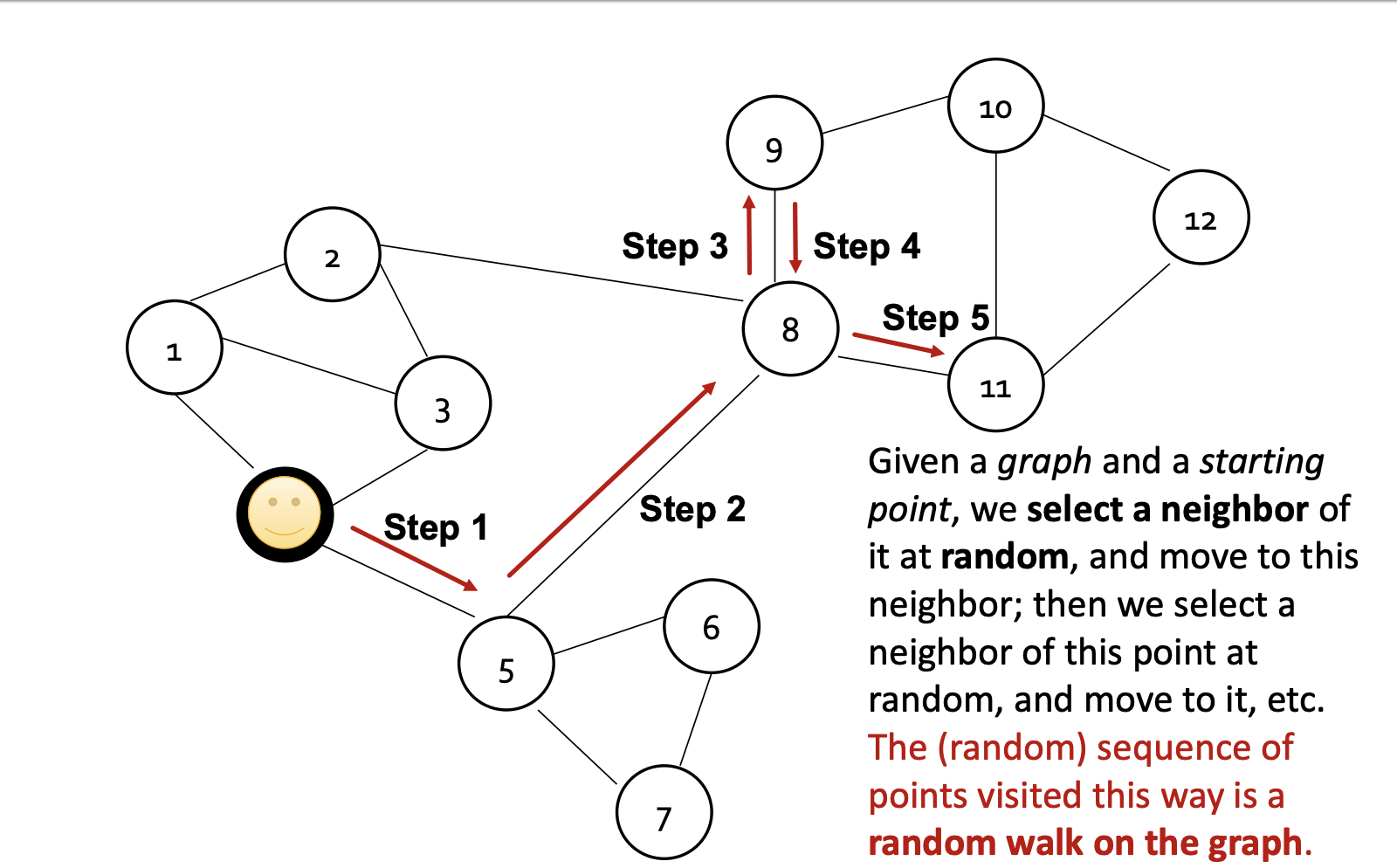
Randomwalk 방법은 주어진 그래프에서 특정 노드에서 random한 노드를 선택하여 neighbor 를 결정하는 방법이다.
node u 에서 출발하여 node v 에 도착할 확률은 $ {p_R(u|v)} $ 로 표현 할 수 있으며 가까운 노드 사이의 embedding distance를 최소화하는 식으로 optimize embedding을 한다.
그렇다면 node ${u}$ 가 주어졌을 때, nearby 노드들을 어떤 식으로 표현해야 할까?
random walk에서는 node u에서 v 까지의 sequence 에 속한 노드 집합들을 ${N_R(u)}$ 라고 정의한다.
node ${u}$가 주어졌을 때, ${N_R(u)}$ 을 예측해야 한다.
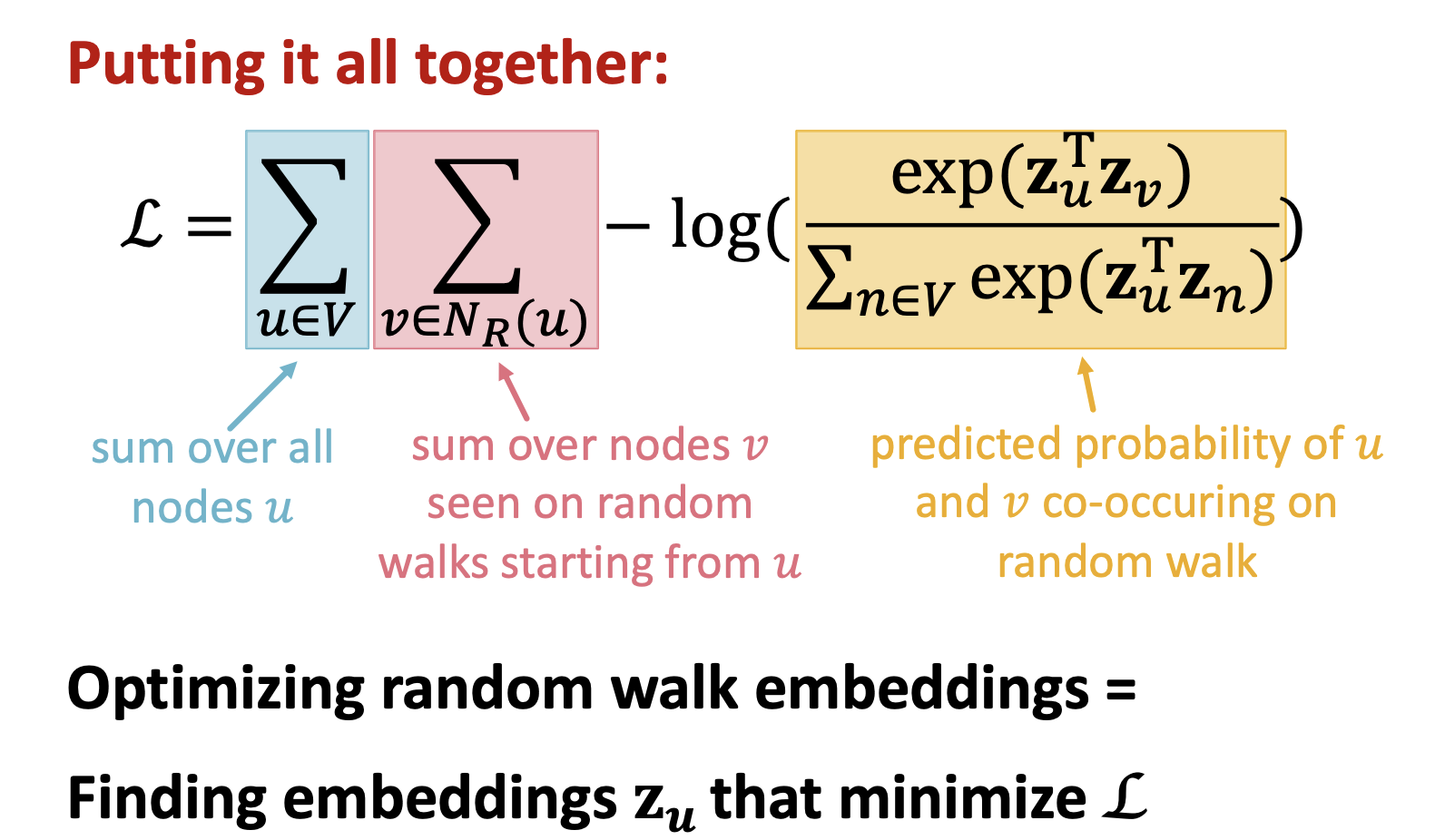
Loss function을 다음과 같이 설계할 수 있다.
좌항은 node 집합 u 중 random walk를 통해 u에서 v 로 가는 것들이고,
우항은 log-softmax이며, 전체 u의 randomwalk 중에서 v로 가는 것들의 비율이다.
따라서 L 을 최소화하는 embedding 함수 $ z_u $ 를 최적화하는 것이 목적이다.
하지만 식에서 Node summation이 두번이나 있기 때문에 계산 효율성이 좋지는 않다.
이를 해결하기 위해 word2vec 처럼 negative sampling 을 적용한다.
Negative sampling

word2vec 에서 자주 쓰이는 단어 중 주변 단어가 아닌 타겟과 의미가 없는 단어들을 선별적으로 골라서 업데이트하는 것처럼, high degree node를 sample로 선정한다. k는 negative sample numbers.
negative sampling 은 계산의 효율성 외에도 다음과 같은 특징이 있으며 주로 5-20 의 값을 사용한다고 한다.
1. Higher k gives more robust estimates
2. Higher k corresponds to higher bias on negative events
최적화 방법으로는 stochastic gradient descent 기법을 사용한다.

Node2vec
Deepwalk와 비슷하다. 그런데 조금 더 rich embedding을 구해 flexible neighborhood ${N_R(u)}$ 를 정의한다.
네트워크의 local , global view 를 모두 고려하는 flexible,biased random walk 전략을 취한다.
BFS(Breadth-First Search)는 주변 node로 탐색, DFS(depth-first search)는 sequence가 긴 경로를 탐색한다.
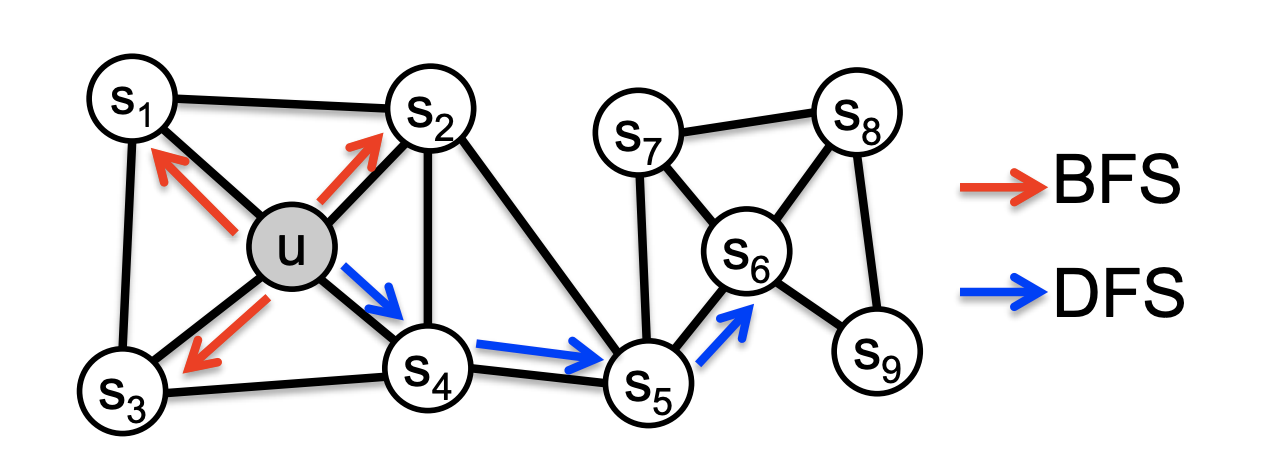
Node2vec 에서는 BFS와 DFS의 ratio 에 해당하는 파라미터 q와, 왔던길을 되돌아가는 p를 추가하여 Biased random walk 집합인 ${N_R(u)}$ 를 정의한다.

알고리즘의 학습 방법은 Deepwalk 와 같다.
1. random walk prob 계산
2. node u 에서 시작하는 길이 l의 random walk simulation
3. SGD를 통해 node2vec 목적 함수 optimize
3. Embedding Entire Graphs
그렇다면 노드 단위의 임베딩이 아닌 그래프 자체 또는 subgraph 의 임베딩은 어떻게 해야할까?
노드 단위가 아닌 그래프 단위가 단일 객체를 나타내는 가령 moecules classification 나
그래프 단위의 이상탐지 등의 task 는 그래프를 임베딩해야 한다.
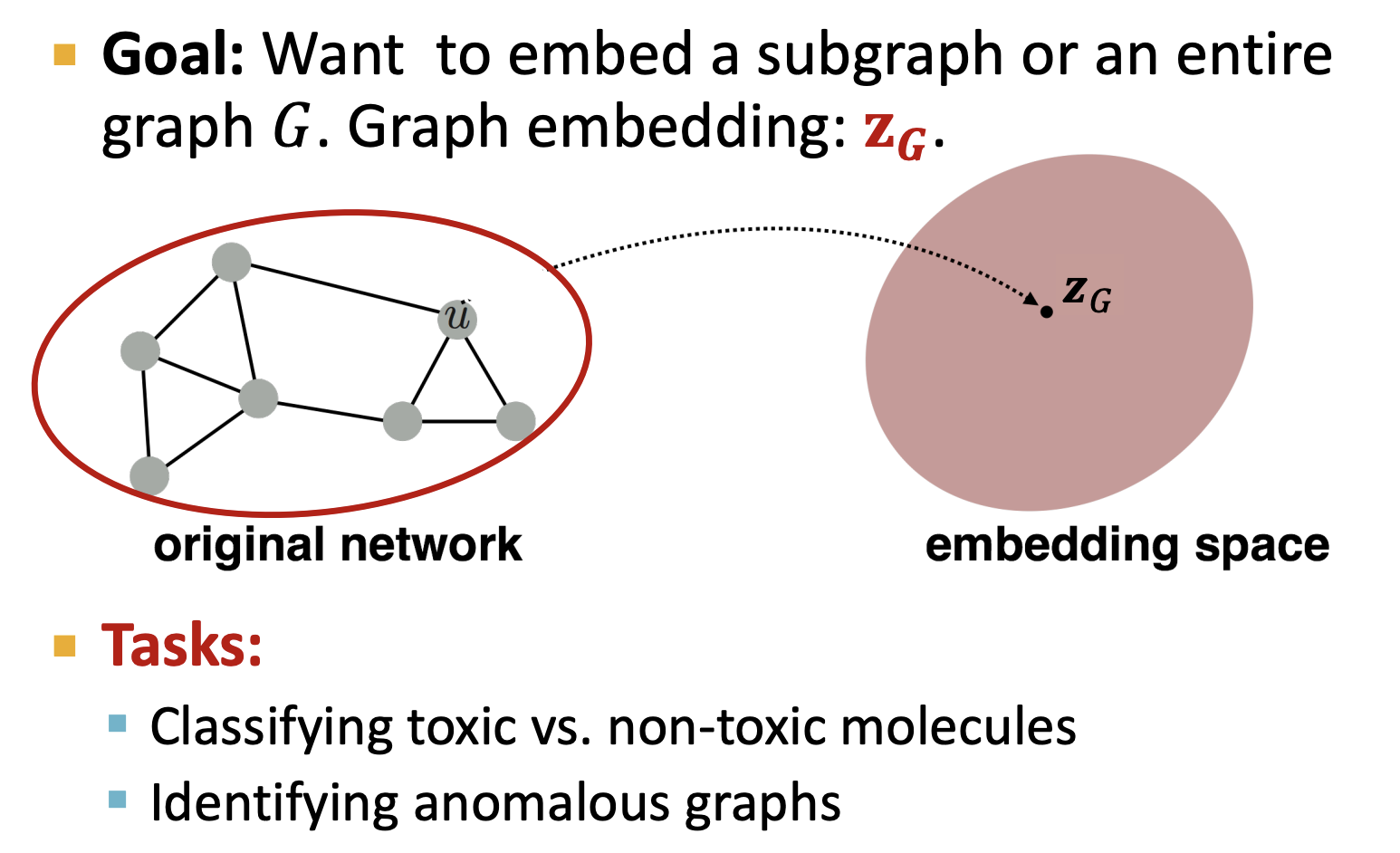
- Simple Idea 1
가장 간단한 방법은 하위 그래프 혹은 노드 임베딩의 합으로 그래프를 임베딩을 표시하는 것이다.

- Idea 2 : 그래프 내부에 "virtual node" 를 추가하여 기존의 그래프 임베딩 기법으로 이 노드에 virtual node 가 cover하는 subgraph에 대한 정보를 담는다. 그럼 전체 그래프 임베딩은 virtual node 들의 합으로 구하나..

- Idea3 : anonymous walks는 그래프의 노드별 순서를 특정 노드별이 아닌 인덱스별로 표시한다.
가령 아래 그림처럼 A-B-C 도 1-2-3, C-D-B도 1-2-3 이다.

Summary
graph representation learning 을 하는데 있어 피쳐 엔지니어링 없이 node, graph classification, link prediction 등의 task에 사용할 수 있는 node, graph embedding에 대해서 알아봤다.
- Encoder-decoder framework
Encoder : 단순한 임베딩 lookup
Deocder : node similarity 를 계산하기 위해 임베딩을 통해 score 계산 (u-v Softmax) - Node similarity measure : (biased) random walk
Deepwalk : 1st order random walk , Node2Vec : 2nd order, exploration fine-tune 가능 - Extension to Graph embedding :
노드 임베딩에 대한 aggregation, anonymous walk embedding
Reference
- Graph represent learning
https://www.cs.mcgill.ca/~wlh/grl_book/
Graph Representation Learning Book
The field of graph representation learning has grown at an incredible (and sometimes unwieldy) pace over the past seven years, transforming from a small subset of researchers working on a relatively niche topic to one of the fastest growing sub-areas of de
www.cs.mcgill.ca
- CS224W
https://www.youtube.com/results?search_query=cs224w
'Graph' 카테고리의 다른 글
| 06. Structural properties of Network (0) | 2022.06.04 |
|---|---|
| 05. Node centrality rating on Networks (0) | 2022.06.01 |
| [CS224W] 7. Graph Neural Networks 2: Design Space (0) | 2022.02.26 |
| Graph Convolutional Network (GCN) (0) | 2022.02.22 |
| [CS224W] 5. Label Propagation for Node Classification (0) | 2022.02.08 |
댓글
이 글 공유하기
다른 글
-
05. Node centrality rating on Networks
05. Node centrality rating on Networks
2022.06.01 -
[CS224W] 7. Graph Neural Networks 2: Design Space
[CS224W] 7. Graph Neural Networks 2: Design Space
2022.02.26 -
Graph Convolutional Network (GCN)
Graph Convolutional Network (GCN)
2022.02.22 -
[CS224W] 5. Label Propagation for Node Classification
[CS224W] 5. Label Propagation for Node Classification
2022.02.08