Asymmetric Loss For Multi-Label Classification 리뷰
Asymmetric Loss For Multi-Label Classification
안녕하세요 오늘 리뷰 할 논문은 Asymmetric Loss For Multi-Label Classification로 줄여서 ASL Loss라고 합니다.
6개월 전쯤에 패션 스타일 데이터의 multi label 문제를 풀다가 paperwithcode 에서 당시 2위로 높은 순위를 기록하고 있길래 적용을 했는데 좋은 효과를 보아서 소개하려고 합니다.
저도 그랬지만 주위에서 Data imbalance 문제를 겪는 문들을 많이 봤습니다. 보통은 upsampling을 쓰는 smote 기법이나 undersampling 등을 많이 사용하지만 크게 효과를 보지는 못하는 것 같습니다. 그중에서도 focal loss가 좀 더 좋다고 알려져 있지만 논문에 따르면 focal loss보다 더 좋은 성능을 보인다고 합니다. 실제로 제가 GCN, focal loss와 함께 학습한 결과를 비교해봤을 때도 가장 성능이 좋았습니다.
잘못 이해한 부분이 있다면 댓글 부탁드립니다.
1. Introduction
이미지 분류뿐만 아니라 객체 탐지에서도 positive class의 부족으로 인한 정확도 하락이 존재해왔습니다. 최근 논문중에는 GCN 등, 사전학습된 워드 임베딩을 이용하여 그래프 신경망으로 라벨 간의 상관관계를 학습시키는 방법들이 있지만 저자는 이런 external information 없이도 loss fucntion의 디자인만으로 성능 향상을 할 수 있다고 말합니다.
[Abstract]
This positive-negative imbalance dominates the optimization process, and can lead to under-emphasizing gradients from positive labels during training, resulting in poor accuracy. In this paper, we introduce a novel asymmetric loss (”ASL”), which operates differently on positive and negative samples. The loss enables to dynamically down-weights and hard-thresholds easy negative samples, while also discarding possibly mislabeled samples
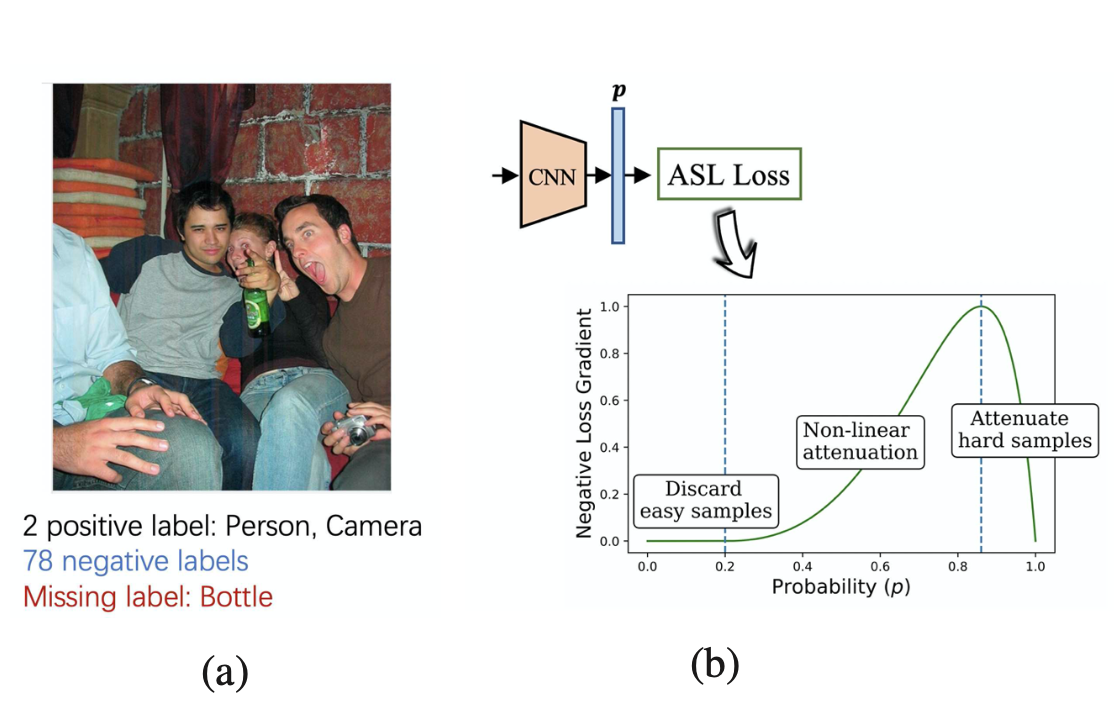
Contribution
- ASL로 negative-positive imbalance, mislabeling 해결
- 기존 아키텍쳐 구조를 변경하지 않기 때문에 모델 학습시간이나 추론 시간의 부하는 없으면서 성능이 좋다
2.1. Binary Cross-Entropy and Focal Loss
Asymmetric Loss 를 살펴보기 전에 , 기존의 대표적인 손실 함수인 cross entropy loss와 focal loss를 살펴보겠습니다. focal loss는 class imbalance 가 있는 데이터셋에 효과적이라고 알려져 있는데 왜 그럴까요. 수식을 간략히 하기 위해서, 이진 분류 문제라고 가정하겠습니다. +- 는 각각 positive, negative sample에 관한 Loss입니다.
- Cross Entropy Loss
- $L = -yL_{+} - (1-y)L_{-}$
- $L = -yL_{+} - (1-y)L_{-}$
- Focal Loss
- $L_+ = (1-p)^{\gamma}log(p)$
Asymmetric loss에서는 positive, negative example loss를 구분하므로 원 논문 표기인 $FL(p_t) = -(1-p_t)^{\gamma} log(p_t)$와는 살짝 식이 다릅니다. 다음은 Focal Loss 논문의 Figure입니다.
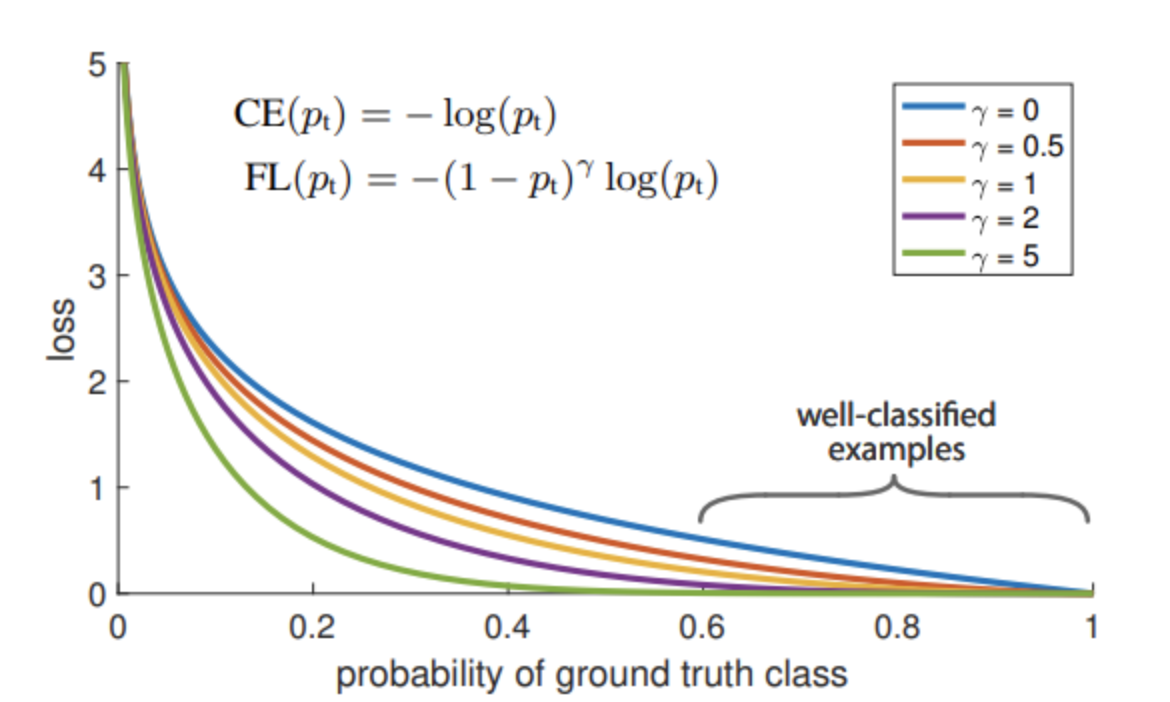
$\gamma=0$ , 일 때는 결국 CE의 수식과 같으므로 크로스 엔트로피와 감마승을 적용한 Focal loss의 loss 차이를 비교하는 그래프입니다.
문제는 ground truth (y) > 0.6 이상일 때의, 분류하기가 상대적으로 쉬운 well-classified easy case의 loss 가 생각보다 작지 않다는 것입니다.
그럼 클래스 분포를 고려해서 가중치를 다르게 주면 되지 않을까?
그래서 시도된 Balanced Cross Entropy의 목적은, 데이터셋의 클래스 비율을 고려하여 하이퍼 파라미터 a를 곱해주어 이진 분류 시 loss 값의 업데이트를 다르게 하겠다는 점에 있습니다.
$$CE(p_t) = -{\alpha}_t log(p_t)$$
이제 다시 Focal loss 공식을 보면 modulating factor인 $-(1-p_t)^{\gamma}$ 가 balanced weight의 맥락으로 이해할 수 있습니다. 어떤 식으로 example의 학습을 조절하는지 보겠습니다.
1. high pt: pt가 크고, well-classified examples 인 경우, modulating factor는 0에 가까워지고, focusing parameter인 ${\gamma}$ 값이 커질수록 loss 가 줄어듭니다. 즉, easy example에 대한 down-weight를 한다고 볼 수 있습니다.
2. low pt : pt가 작고, example 이 잘못 분류될 때, modulating factor 가 1에 가까워지므로, loss의 영향은 반대의 경우보다 상대적으로 적습니다. 기존 $CE = log(p_t)$ 식과 비교했을 때, 잘못 분류된 경우에도 loss가 줄어들기 때문에 영향이 없는 건 아닙니다. 이건 focal loss의 trade-off로 이해할 수 있습니다.

r=5로 조금 극단적인 예시를 들어 0.05~1.0 의 pt 일 때, low, high pt (0.3,0.8) 을 잡아 비교해봤더니 약 1500배정도 차이가 났습니다. 감마 값에 따라서 차이가 나겠지만, focal loss 는 negative easy example 에 집중한다고 볼 수 있습니다.
정리하자면 "Focal loss는 easy example을 down-weight하여 hard negative sample에 집중하여 학습하는 loss function이다"
2.2. Asymmetric Focusing
논문에서는 Asymmetric loss 를 정의하기에 앞서, Asymmetric focusing 과 probability shifting 두 가지를 소개합니다. 앞서 Focal loss 는 easy negative samples를 down-weight 하지만 여기서 발생하는 tradeoff 를 논문에서는 지적합니다.
Focal loss may eliminate the gradients from the rare positive samples. We propose to decouple the focusing levels of the positive and negative samples
rare positive samples 즉, 잘 분류하지 못하는 low pt 인 경우, gradient 손실이 있을 수 있으니 positive, negative samples를 분리해서 생각해야 한다고 말합니다. 자꾸 L+ ,L- 를 나눠서 표기하는 이유가 여기에 있습니다.
- $L_+ = (1-p)^{r_+}log(p)$
- $L_- = p^{r_-}log(1-p)$
위의 focal loss 수식과 같지만 r+ ,r- 입니다. 항상 r- > r+ 로 설정하여, postive examples 의 decay rate를 다르게 학습시켜, 기존에 rare positive exmaples 이 제외되는 경우를 방지시키기 위함입니다.
2.3. Asymmetric Probability Shifting
Asymmetric focusing reduces the contribution of negative samples to the loss when their probability is low (soft thresholding)
앞서 말한, asymmetric focusing (soft thresholding) 방법을 적용했을 때, 매우 imbalance가 큰 상황을 가정하면 negative samples 의 학습이 잘 안되는 문제가 있을 수 있어서 항상 효과적이진 않습니다. 따라서 이를 보완하는 hard thresholding 방법을 추가하려고 합니다.
$$p_m = max(p-m,0)$$
간단한 식으로 margin 을 0.2 로 설정하면, 0.2 이하의 low pt 들은 죄다 0이 됩니다.
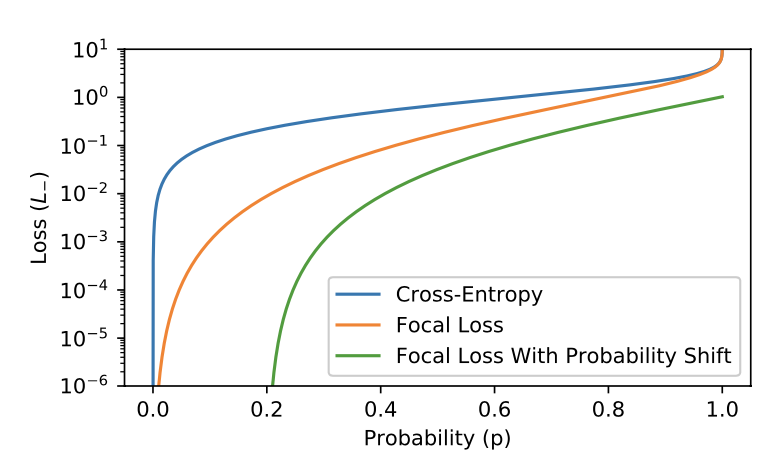
we propose an additional asymmetric mechanism, probability shifting, that performs hard thresholding of very easy negative samples
⇒ negative sample을 학습할 때 pt 가 가장 낮은 것들을 학습에서 제외시킴으로써 Asymmetric Focusing 의 단점을 보완했습니다. 이제 ASL 를 정의할 수 있습니다.
2.4 ASL Definition
앞서 설명한 asymmetric focusing 과 probability shifting 개념을 사용합니다. 앞의 내용을 이해했다면 쉽게 이해할 수 있습니다.
Asymmetric Loss
- $L_+ = (1-p)^{\gamma_+}log(p)$
- $L_- = p_m^{\gamma_-} log(1-p_m)$
3. Experiment
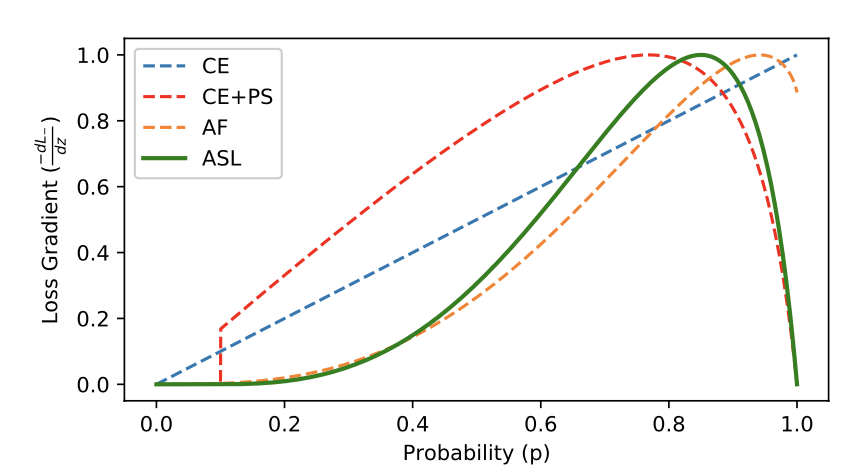
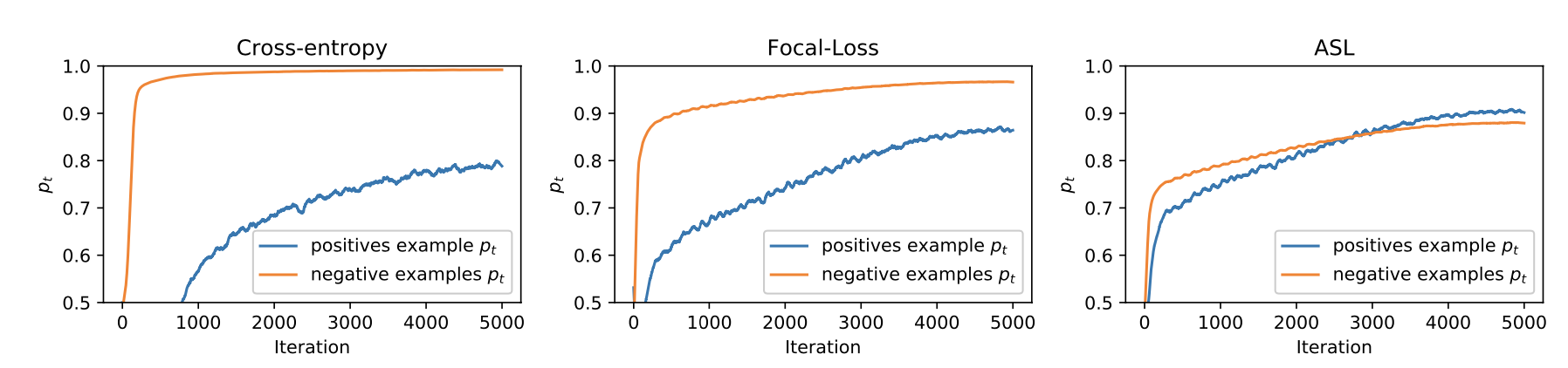
4. Code
class AsymmetricLoss(nn.Module):
def __init__(self, gamma_neg=4, gamma_pos=1, clip=0.05, eps=1e-8, disable_torch_grad_focal_loss=True):
super(AsymmetricLoss, self).__init__()
self.gamma_neg = gamma_neg
self.gamma_pos = gamma_pos
self.clip = clip
self.disable_torch_grad_focal_loss = disable_torch_grad_focal_loss
self.eps = eps
def forward(self, x, y):
""""
Parameters
----------
x: input logits
y: targets (multi-label binarized vector)
"""
# Calculating Probabilities
x_sigmoid = torch.sigmoid(x)
xs_pos = x_sigmoid
xs_neg = 1 - x_sigmoid
# Asymmetric Clipping
if self.clip is not None and self.clip > 0:
xs_neg = (xs_neg + self.clip).clamp(max=1)
# Basic CE calculation
los_pos = y * torch.log(xs_pos.clamp(min=self.eps))
los_neg = (1 - y) * torch.log(xs_neg.clamp(min=self.eps))
loss = los_pos + los_neg
# Asymmetric Focusing
if self.gamma_neg > 0 or self.gamma_pos > 0:
if self.disable_torch_grad_focal_loss:
torch.set_grad_enabled(False)
pt0 = xs_pos * y
pt1 = xs_neg * (1 - y) # pt = p if t > 0 else 1-p
pt = pt0 + pt1
one_sided_gamma = self.gamma_pos * y + self.gamma_neg * (1 - y)
one_sided_w = torch.pow(1 - pt, one_sided_gamma)
if self.disable_torch_grad_focal_loss:
torch.set_grad_enabled(True)
loss *= one_sided_w
return -loss.sum()'machine learning > Article review' 카테고리의 다른 글
| Hybrid- Swin-Transformers 리뷰 (0) | 2021.12.24 |
|---|---|
| Intriguing properties of vision transformer 리뷰 (0) | 2021.12.24 |
| BERT4Rec review (0) | 2021.12.19 |
| YOLO v1 리뷰 (0) | 2021.12.16 |
| Fast & Faster R-CNN 리뷰 (0) | 2021.12.03 |
댓글
이 글 공유하기
다른 글
-
Hybrid- Swin-Transformers 리뷰
Hybrid- Swin-Transformers 리뷰
2021.12.24 -
Intriguing properties of vision transformer 리뷰
Intriguing properties of vision transformer 리뷰
2021.12.24 -
BERT4Rec review
BERT4Rec review
2021.12.19 -
YOLO v1 리뷰
YOLO v1 리뷰
2021.12.16